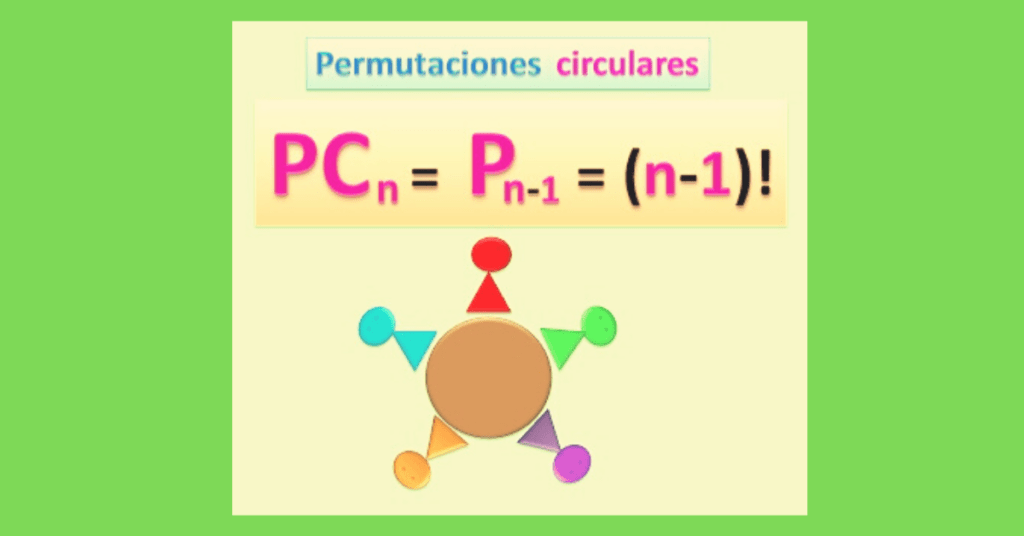
Resolviendo ejercicios de permutación, Es más fácil de lo esperado.
Una permutación, también llamada número de arreglo, es una reorganización de los elementos de una lista ordenada en una correspondencia uno a uno consigo misma.
Aprenderemos la fórmula de permutación para el número de permutaciones de n cosas tomadas r a la vez. También aprenderemos cómo resolver problemas verbales de permutación con símbolos repetidos y problemas verbales de permutación con restricciones o condiciones especiales.
El número de formas de obtener un subconjunto ordenado de r elementos de un conjunto de n elementos viene dado por
P (n,r) = n! / (n-r)!
donde n! es un factorial. Por ejemplo, hay 4!/2! = 12
2-subconjuntos de (1,2,3,4),
a saber (1,2),(1,,3),(1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3),
Los subconjuntos desordenados que contienen r elementos se conocen como los r subcojuntos de un conjunto dado.
En general, P (n,r) significa que el número de permutaciones de n cosas tomadas r a la vez. Podemos usar el razonamiento para resolver este tipo de problemas de permutación o podemos usar la fórmula de permutación.
La fórmula para la permutación es
P (n,r) = n! / (n-r)!
Ejemplo:
Una placa de matrícula comienza con tres letras. Si las letras posibles son A, B, C, D y E, ¿cuántas permutaciones diferentes de estas letras se pueden hacer si no se usa ninguna letra más de una vez?
Solución:
Para la primera letra, hay 5 opciones posibles. Después de elegir esa letra, hay 4 opciones posibles. Finalmente, hay 3 opciones posibles.
5 × 4 × 3 = 60
El problema involucra 5 cosas (A, B, C, D, E) tomadas 3 a la vez.
P (5, 3) = 5! / (5-3)! = 5! / 2! =5*4*3*2! / 2! = 60
Hay 60 permutaciones diferentes para la matrícula.
¿Cómo usar la fórmula de permutación para resolver problemas de palabras?
Ejemplo:
¿De cuántas maneras se puede elegir un presidente, un tesorero y una secretaria entre 7 candidatos?
Para la primera posición, hay 7 opciones posibles. Después de elegir a ese candidato, hay 6 opciones posibles. Finalmente, hay 5 opciones posibles.
7 × 6 × 5 = 210
El problema involucra a 7 candidatos tomados 3 a la vez.
P (7, 3) = 7! / (7-3)! = 7! / 4! =7*6*5*4! / 4! = 210
Hay 210 formas posibles de elegir un presidente, un tesorero y una secretaria entre 7 candidatos
Ejemplo:
Un código postal contiene 5 dígitos. ¿Cuántos códigos postales diferentes se pueden hacer con los dígitos 0–9 si no se usa ningún dígito más de una vez y el primer dígito no es 0?
Para la primera posición, hay 9 opciones posibles (ya que 0 no está permitido). Después de elegir ese número, hay 9 opciones posibles (ya que ahora se permite 0). Luego, hay 8 opciones posibles, 7 opciones posibles y 6 opciones posibles.
9 × 9 × 8 × 7 × 6 = 27216
No podemos incluir el primer dígito en la fórmula porque 0 no está permitido.
Para la primera posición, hay 9 opciones posibles (ya que 0 no está permitido). Para las siguientes 4 posiciones, estamos seleccionando entre 9 dígitos.
9*P (9, 4) = 9* 9! / (9-4)! = 9*9! / 5! =9*87*6*5 / 5! = 27216
Ejemplo:
¿De cuántas maneras diferentes pueden alinearse 3 estudiantes para comprar un nuevo lector de libros de texto?
n-factorial da el número de permutaciones de n elementos = n (n – 1) (n – 2) (n – 3) … (3) (2) (1)
Permutaciones de n elementos tomados r a la vez.
P (n, r) representa el número de permutaciones de n elementos r a la vez.
P (n, r) = n! / (n-r)!
Ejemplos:
- Encuentra P (7,3) y P (15,5)
- ¿De cuántas maneras se pueden ordenar las letras de la palabra PHOENIX?
- ¿De cuántas maneras se pueden organizar las letras de la palabra MATEMÁTICAS?
- ¿Cómo calcular el número de arreglos lineales de la palabra MISSISSIPPI (las letras del mismo tipo no se pueden distinguir)?
